Ringdown 1/e² Calculator
Cavity ringdown spectroscopy measures the rate of optical energy decay in a resonant cavity to determine properties like mirror reflectivity, absorption, or molecular concentration. The diagram below illustrates this process:
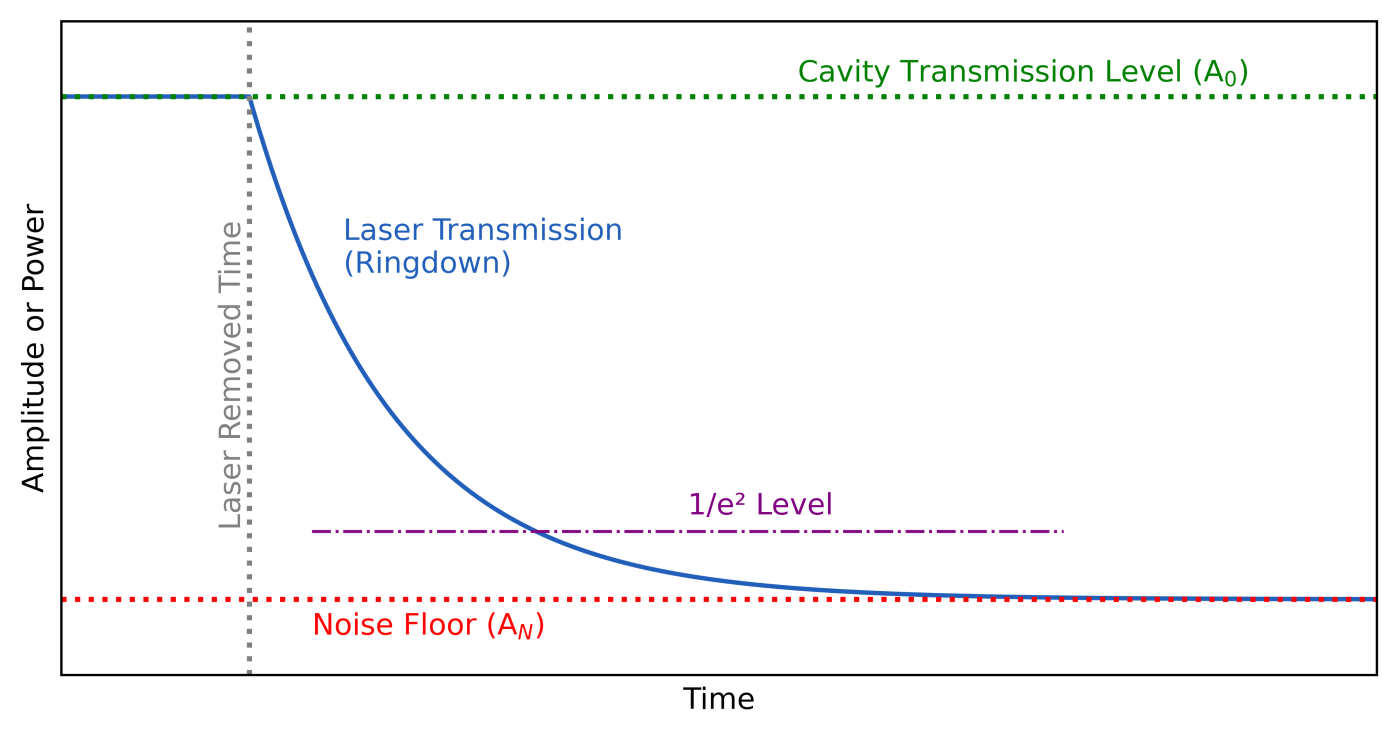
In a typical setup, an acousto-optic modulator (AOM) is used to switch off the laser input to the cavity rapidly. When the laser is on, light builds up in the cavity when in resonance (green dotted line). At time $t=0$, the AOM deflects the beam, preventing new light from entering the cavity. The light trapped inside the cavity then "rings down" exponentially (blue curve) toward the detector's noise floor (red dotted line).
The AOM works by creating an acoustic wave in a crystal, forming a diffraction grating that can deflect the laser beam in microseconds. By turning off the RF signal to the AOM, the first-order diffracted beam (which feeds the cavity) is extinguished, allowing measurement of the pure decay time.
This calculator determines the $\frac{1}{e^2}$ level, the point where the signal has decayed to approximately 13.5% of its initial value above the noise floor. This specific level is often used in cavity ringdown measurements to determine the cavity decay time constant τ, which relates to the cavity finesse and mirror reflectivity.