Robust Optimal Control for LIGO
The Buzz Package
June 11, 2025
One of the biggest challenges in detecting gravitational waves is noise. At the Laser Interferometer Gravitational-wave Observatory (LIGO), even tiny disturbances can mask the faint signals from colliding black holes or neutron stars. At low frequencies, below ~30 Hz, LIGO’s sensitivity is dominated by “controls noise,” the byproduct of the feedback loops that keep the detector’s many suspended mirrors precisely aligned.
Much of this contamination is driven by nonlinear couplings, especially bilinear noise, where disturbances in different parts of the control system multiply and leak into the gravitational-wave readout. Because there’s no known lower bound to bilinear noise, smarter controller design can drive it substantially lower than hand-tuned loops.
I built a mixed Linear Quadratic Gaussian (LQG) and H-infinity control framework to push that noise down while keeping the stability margins required on a real instrument. LQG provides globally optimal noise suppression for specified figures of merit; the H-infinity bound guarantees robust gain/phase margins by directly capping gain peaking.
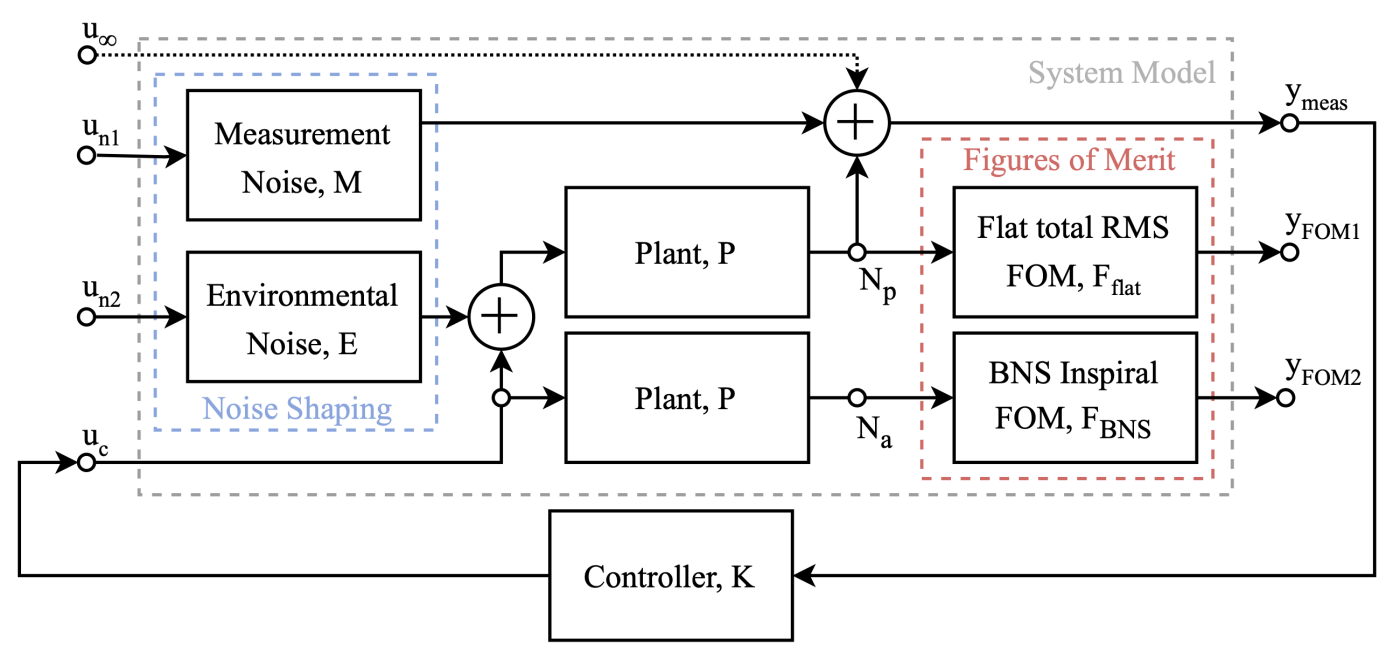
Caption: System model used for optimization. Noise enters as shaped “environmental” and “measurement” disturbances, flows through the plant and controller, and is evaluated by two figures of merit: (i) flat RMS for operational lock and (ii) BNS-weighted RMS for astrophysical reach.
Applying this framework to LIGO’s alignment system, specifically the DHARD yaw mode, I computed families of optimal controllers that reveal the true performance limits for linear control. The core result is a robust set of designs that retain LQG’s noise reduction while meeting strict stability margins imposed via the H-infinity bound.
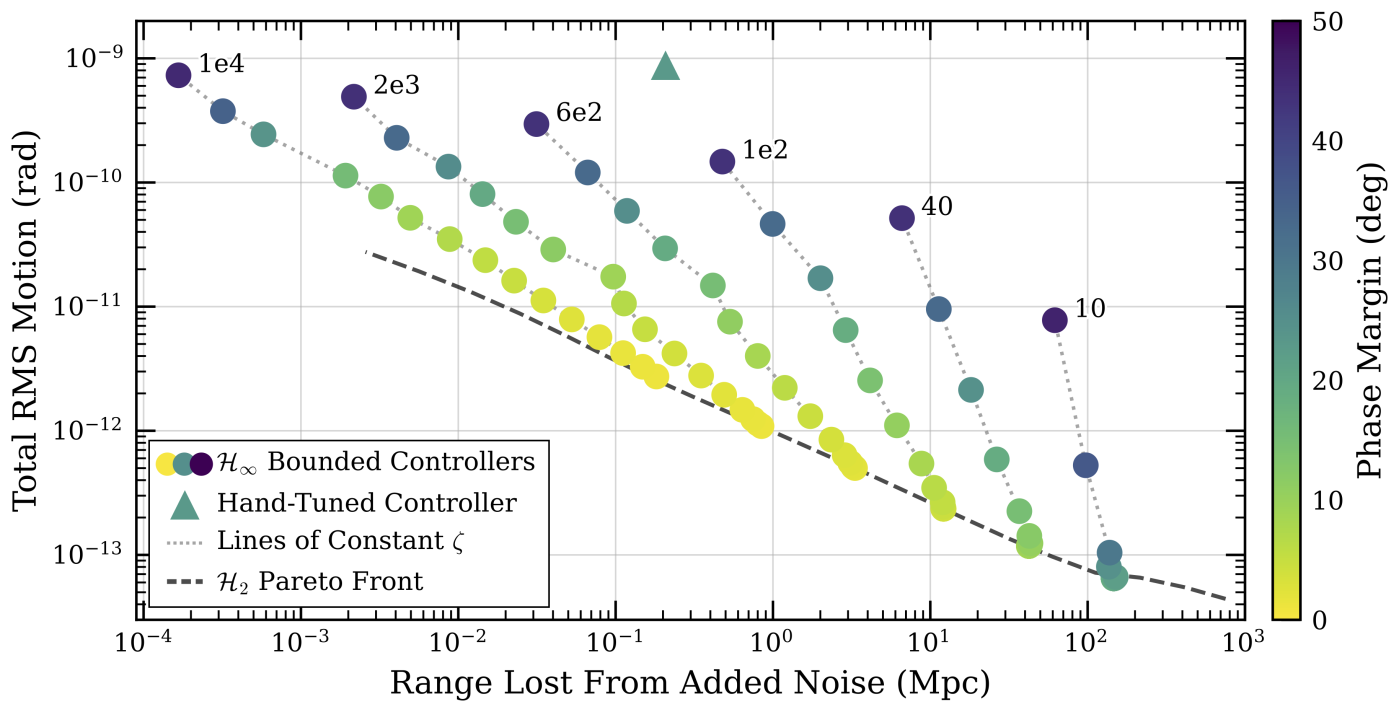
Caption: RMS performance with $\mathcal{H}_\infty$ bounds. Each point is an optimal controller for a particular weighting of the two figures of merit. The curve shows the achievable trade-off frontier; compared to the current hand-tuned controller, the robust designs reduce total RMS substantially while preserving stability.
A key to making these controllers deployable is controlling gain peaking (and thus phase margin). The open-loop view shows how the controller shapes gain to suppress environmental disturbances at low frequency without over-exciting high-frequency sensor noise.
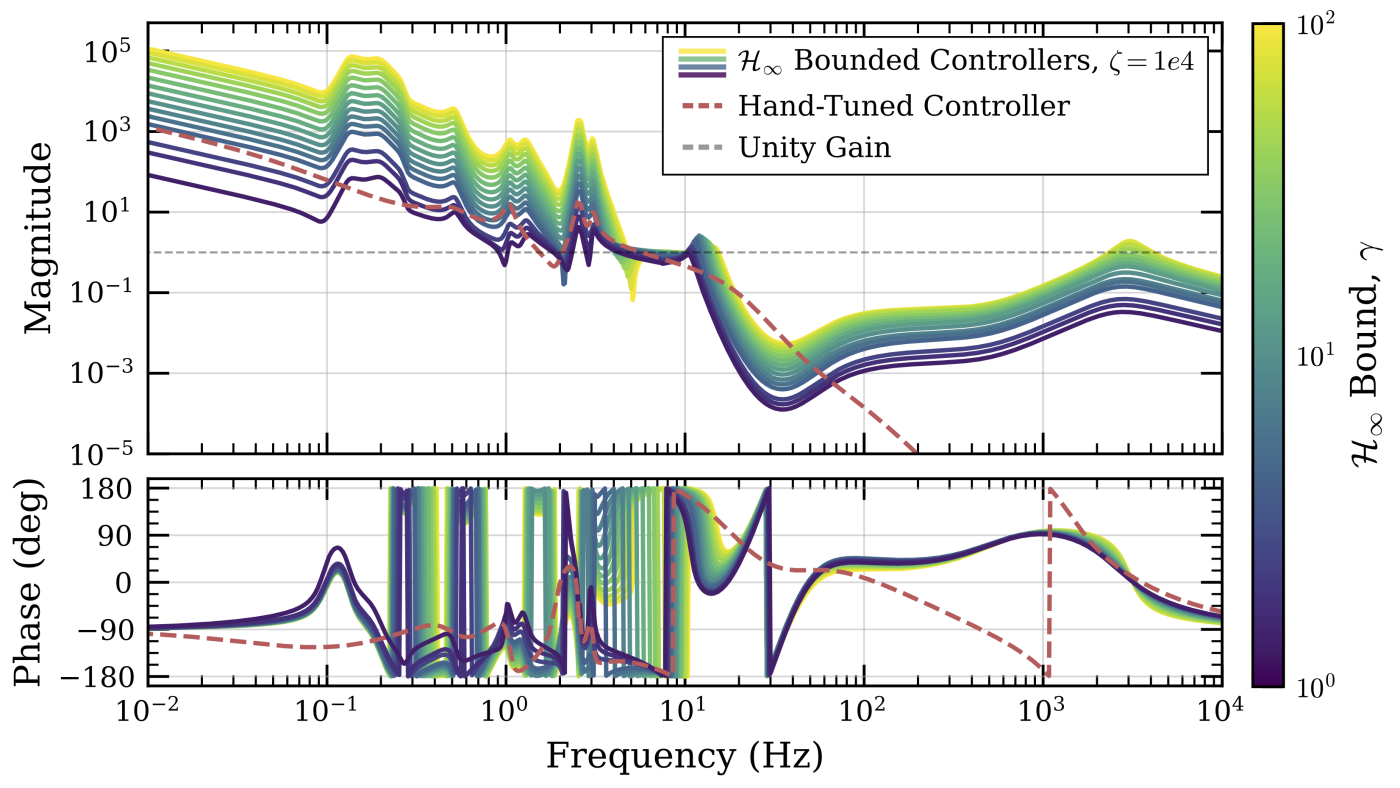
Caption: Open-loop gain of $\mathcal{H}_\infty$-bounded controllers. As the stability bound tightens, the solution maintains authority where it matters (near unity gain) but avoids overly aggressive shaping that would degrade margins.
The closed-loop transfer further shows the effect of the H-infinity constraint: by directly limiting the closed-loop peak, we enforce acceptable phase margins and avoid fragile “near-edge” designs.
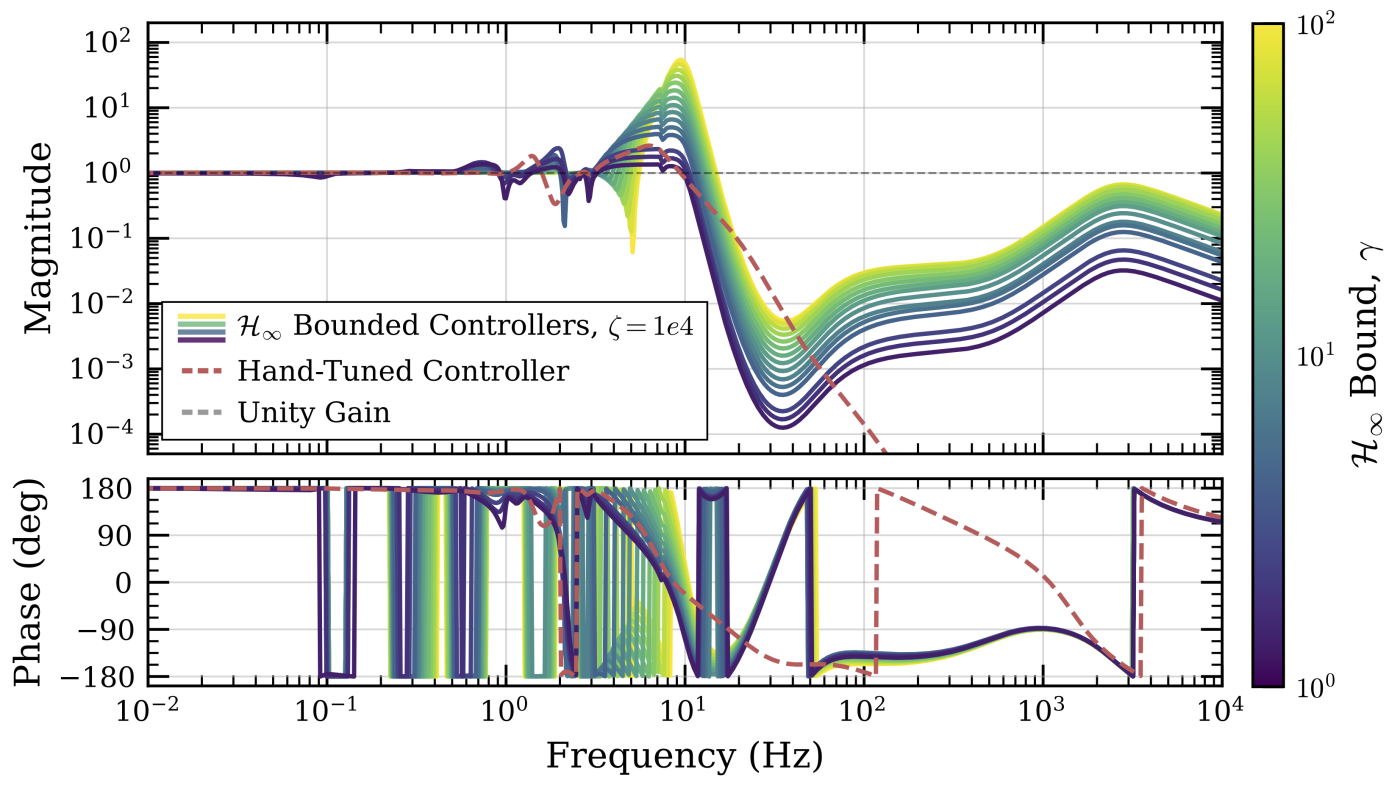
Caption: Closed-loop gain with gain-peaking suppressed. Tighter bounds pull down the peak, translating into healthier phase/gain margins suitable for on-instrument operation.
In practice, these robust optimal controllers achieved a reduction of up to ~50% in total RMS motion relative to the existing DHARD yaw loop, while satisfying stability requirements. That improvement directly supports better low-frequency sensitivity and stronger astrophysical reach.
Beyond this specific loop, the same method sets principled noise requirements and produces globally optimal, robust controllers for other LIGO subsystems, and for next-generation observatories where nonlinear couplings are a limiting factor.